Introduction

I’ve been recently trying to learn more about databases. I’ve been reading through Database Internals and trying to actually implement it in code, because for me that’s the only way I really understand anything.

Implementation In Python

I picked Python for the implementation because I’m most familiar with it, and I wanted to get something working quickly. I’m not sure if I’ll actually use Python for the final implementation eventually when I try to write this to disk, but we’ll see.

I started by asking ChatGPT to implement a B+-Tree for me which involved pagination but it turned into a giant turd. You can look at ChatGPT’s implementation here. I’m not going to go into the details of the implementation, but I will say that it’s not very good. There are many, many errors and I wasted days trying to understand the code when it simply didn’t work.

A Cell In A B+-Tree

The most important thing (atleast for me) when implementing a B+-Tree is to understand what a cell is. A cell is a key-value pair. The key is the value that you’re searching for, and the value is the actual data that you’re storing.

Most online implementations ignore this aspect of the B+-Tree and I think it makes the implementation much more confusing.

There are two types of nodes in a B+-Tree - internal nodes and leaf nodes. Internal nodes are nodes that contain keys and pointers to other nodes. Leaf nodes are nodes that contain keys and values.

Here are some beautifully detailed images of a leaf node and internal node from this blog (Note: I highly recommend reading that blog post!)

A leaf node format:

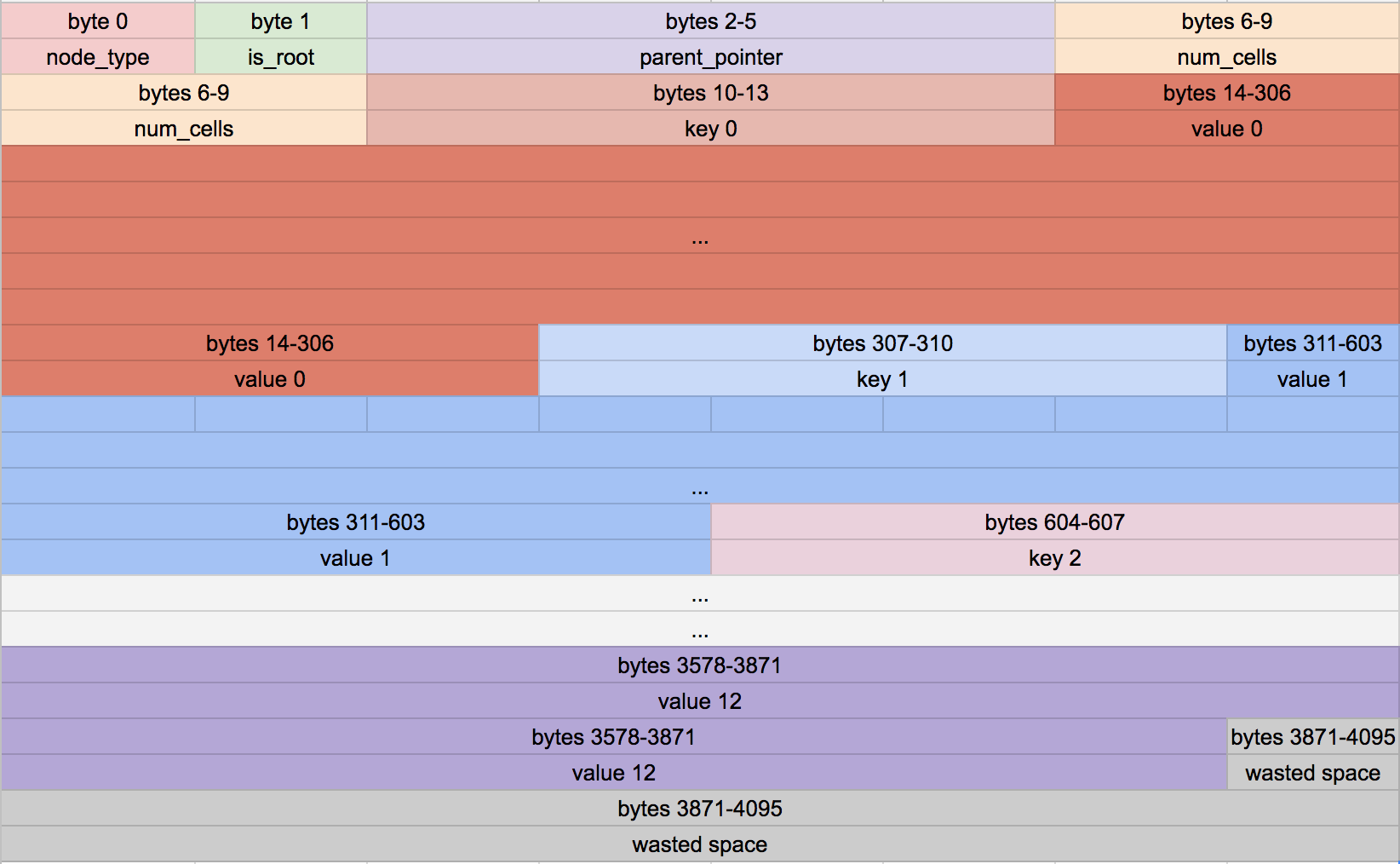
An internal node format:

Since I was writing this in Python I didn’t worry too much about making sure that each node occupies one page of memory. All of that will come later when I write it in a language that actually gives me access to memory (like C).

Inserting A Cell

I’m only going to cover this portion of the algorithm because it’s the only interesting part.

The following section is from Database Internals

Here’s the relevant code

def insert(self, key, value):
        node, index = self._search(key)

        #   If the key already exists in the database
        if index < len(node.cells) and node.cells[index].key == key:
            node.cells[index].value = value
            return True
        
        #   If the key does not currently exist in the database
        self._insert(node, key, value)

    def _insert(self, node, key, value):
        #   Check if the node is full
        insertion_index = bisect_left(node.cells, key, key=lambda x: x.key)
        if node.type is NodeType.LEAF and node.num_of_cells < self.order - 1:
            #   This node will not overflow, add the key value pair
            node.cells.insert(insertion_index, LeafNodeCell(key, value))
            node.num_of_cells += 1
            return node

        if node.type is NodeType.INTERNAL and node.num_of_cells < self.order - 1:
            node.cells.insert(insertion_index, InternalNodeCell(key, value))
            node.num_of_cells += 1
            return node
        
        #   This node will overflow
        
        #   If this node is the root node
        if node.parent is None:
            #   Create a new root node
            new_root = BTreeNode(NodeType.INTERNAL)
            node.parent = new_root
            self.root = new_root

        #   Create a new sibling node first and move half the elements from the current node to the sibling node
        temp_node_cells = node.cells[:]
        sibling_node = BTreeNode(node.type)
        middle_index = node.num_of_cells // 2
        node.cells = node.cells[:middle_index]
        sibling_node.cells = temp_node_cells[middle_index:]
        node.num_of_cells = len(node.cells)
        sibling_node.num_of_cells = len(sibling_node.cells)

        if node.type is NodeType.LEAF:
            #   Place the key into the correct node
            if insertion_index <= middle_index:
                node.cells.insert(insertion_index, LeafNodeCell(key, value))
                node.num_of_cells += 1
            else:
                sibling_node.cells.insert(insertion_index - middle_index, LeafNodeCell(key, value))
                sibling_node.num_of_cells += 1

            key_to_promote = sibling_node.cells[0].key
            parent_node = self._insert(node.parent, key_to_promote, sibling_node)
            node.parent = parent_node
            sibling_node.parent = parent_node
            parent_node.left_child_pointer = node

        if node.type is NodeType.INTERNAL:
            #   Place the key into the correct node
            if insertion_index <= middle_index:
                node.cells.insert(insertion_index, InternalNodeCell(key, value))
                node.num_of_cells += 1
            else:
                sibling_node.cells.insert(insertion_index - middle_index, InternalNodeCell(key, value))
                sibling_node.num_of_cells += 1

            key_to_promote = sibling_node.cells[0].key
            parent_node = self._insert(node.parent, key_to_promote, sibling_node)
            node.parent = parent_node
            sibling_node.parent = parent_node
            parent_node.left_child_pointer = node
            
            if insertion_index <= middle_index:
                return node
            return sibling_node

It’s a massive function and it took me days of effort to finally get this working somewhat correctly. I’m sure there might be some small bugs here and there, but I’m not going to worry about them for now.

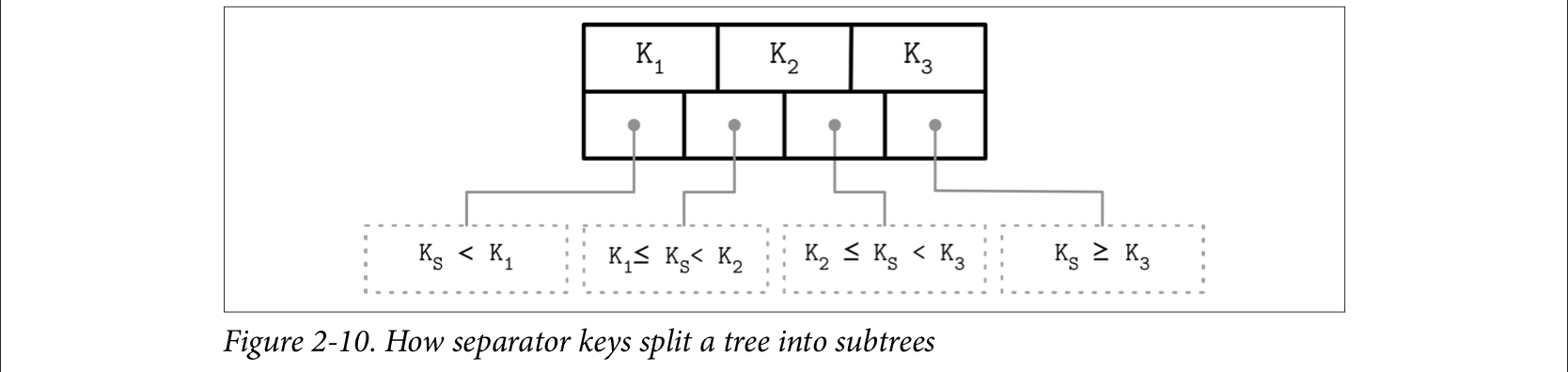
One of the confusing things about different online implementations is, they don’t specify whether each range separate in an internal node is left inclusive or right inclusive. In my implementation, the range separator is left inclusive and not right inclusive.

Here’s a visual representation:

Conclusion

Still a long way away from having something that really works as a simple, dumb DB engine but the storage layer is the first part. So, we’ll see how far I can get.

If you want to take a look at the repository with the full implementation so far, you can find it here