Updating B+ Tree Implementation
Introduction
Last time I shared how I attempted to implement B+ trees in Python. While it was partially successful, there were some obvious edge cases that I had missed out on.
Problems With Key Invariants
One of the problems was that I was not handling the case of inserting the separator key into the parent node in the case of a node split.
Now, in the new version, I make sure to insert the correct key invariant into the parent node when a node split occurs.
def _insert(self, node, key, value):
# Check if the node is full
insertion_index = bisect_left(node.cells, key, key=lambda x: x.key)
if node.type is NodeType.LEAF and node.num_of_cells < self.order - 1:
# This node will not overflow, add the key value pair
node.cells.insert(insertion_index, LeafNodeCell(key, value))
node.num_of_cells += 1
return node
if node.type is NodeType.INTERNAL and node.num_of_cells < self.order - 1:
node.cells.insert(insertion_index, InternalNodeCell(key, value))
node.num_of_cells += 1
return node
# This node will overflow
# If this node is the root node
if node.parent is None:
# Create a new root node
new_root = BTreeNode(NodeType.INTERNAL)
node.parent = new_root
self.root = new_root
# Create a new sibling node first and move half the elements from the current node to the sibling node
temp_node_cells = node.cells[:]
sibling_node = BTreeNode(node.type)
middle_index = node.num_of_cells // 2
node.cells = node.cells[:middle_index]
sibling_node.cells = temp_node_cells[middle_index:]
node.num_of_cells = len(node.cells)
sibling_node.num_of_cells = len(sibling_node.cells)
if node.type is NodeType.LEAF:
# Place the key into the correct node
if insertion_index <= middle_index:
node.cells.insert(insertion_index, LeafNodeCell(key, value))
node.num_of_cells += 1
else:
sibling_node.cells.insert(insertion_index - middle_index, LeafNodeCell(key, value))
sibling_node.num_of_cells += 1
key_to_promote = sibling_node.cells[0].key
parent_node = self._insert(node.parent, key_to_promote, node)
node.parent = parent_node
sibling_node.parent = parent_node
parent_insertion_index = bisect_left(node.parent.cells, key_to_promote, key=lambda x: x.key) + 1
if parent_insertion_index < len(node.parent.cells):
node.parent.cells[parent_insertion_index].left_child_pointer = sibling_node
else:
node.parent.right_child_pointer = sibling_node
# Update the sibling pointers
temp = node.right_sibling_pointer
node.right_sibling_pointer = sibling_node
sibling_node.right_sibling_pointer = temp
if node.type is NodeType.INTERNAL:
# Place the key into the correct node
if insertion_index <= middle_index:
node.cells.insert(insertion_index, InternalNodeCell(key, value))
node.num_of_cells += 1
else:
sibling_node.cells.insert(insertion_index - middle_index, InternalNodeCell(key, value))
sibling_node.num_of_cells += 1
key_to_promote = sibling_node.cells[0].key
parent_node = self._insert(node.parent, key_to_promote, node)
node.parent = parent_node
sibling_node.parent = parent_node
parent_insertion_index = bisect_left(node.parent.cells, key_to_promote, key=lambda x: x.key) + 1
if parent_insertion_index < len(node.parent.cells):
node.parent.cells[parent_insertion_index].left_child_pointer = sibling_node
else:
node.parent.right_child_pointer = sibling_node
# For an internal node, remove the node's right child pointer
node.right_child_pointer = None
if insertion_index <= middle_index:
return node
return sibling_node
Deleting Keys
In the previous post, I also didn’t really go over deleting keys in the database file and how to handle the case of a node underflow.
In the new version, I have added a method to delete keys from the B+ tree.
def delete(self, key):
node, index = self._search(key)
# If the key does not exist in the database
if index >= len(node.cells) or node.cells[index].key != key:
return False
# If the key exists in the database
self._delete(node, index)
def _delete(self, node, index):
if node.type is NodeType.LEAF:
# If the node has more than the minimum number of cells
# Just delete the required cell and reduce number of cells by 1
if node.num_of_cells > math.ceil(self.order / 2) - 1:
node.cells.pop(index)
node.num_of_cells -= 1
return True
else:
# If the node has the minimum number of cells
# Check if the right sibling shares a parent with the current node
if node.right_sibling_pointer is not None and node.right_sibling_pointer.parent is node.parent:
# Delete the cell and reduce number by 1
node.cells.pop(index)
node.num_of_cells -= 1
# Borrow all the cells from the right sibling
node.cells.extend(node.right_sibling_pointer.cells)
node.num_of_cells += node.right_sibling_pointer.num_of_cells
# Delete the right sibling and remove the separator key from the parent node
parent_index_to_remove = bisect_left(node.parent.cells, node.right_sibling_pointer.cells[0].key, key=lambda x: x.key)
node.right_sibling_pointer = node.right_sibling_pointer.right_sibling_pointer
self._delete(node.parent, parent_index_to_remove)
return True
else:
# If the current node and right sibling do not share a parent and
# removing a cell from the current node will result in less than minimum number of cells
# then just delete the cell. If removing the cell will result in an empty node, remove the # node and update the parent node
temp = node.cells[index].key
del node.cells[index]
node.num_of_cells -= 1
if node.num_of_cells == 0:
parent_index = bisect_left(node.parent.cells, temp, key=lambda x: x.key)
self._delete(node.parent, parent_index)
return True
elif node.type is NodeType.INTERNAL:
# If the node has more than the minimum number of cells
if node.num_of_cells > math.ceil(self.order / 2) - 1:
del node.cells[index]
node.num_of_cells -= 1
return True
else:
# If node has the minimum number of cells
# Check if the right sibling shares a parent with the current node
if node.right_sibling_pointer is not None and node.right_sibling_pointer.parent is node.parent:
# Delete the cell and reduce number by 1
node.cells.pop(index)
node.num_of_cells -= 1
# Borrow all the cells from the right sibling
node.cells.extend(node.right_sibling_pointer.cells)
node.num_of_cells += node.right_sibling_pointer.num_of_cells
# Delete the right sibling and demote the separator key from the parent node into
# the current node
node.right_sibling_pointer = node.right_sibling_pointer.right_sibling_pointer
parent_index_to_demote = bisect_left(node.parent.cells, node.right_sibling_pointer.cells[0].key, key=lambda x: x.key)
parent_cell_to_demote = node.parent.cells[parent_index_to_demote]
node_insertion_index = bisect_left(node.cells, node.parent.cells[parent_cell_to_demote].key, key=lambda x: x.key)
node.cells.insert(node_insertion_index, node.parent.cells[parent_cell_to_demote])
node.num_of_cells += 1
self._delete(node.parent, parent_index_to_demote)
else:
# If the current node and right sibling do not share a parent and
# removing a cell from the current node will result in less than minimum number of cells
# then just delete the cell. If removing the cell will result in an empty node, remove the node
# and update the parent node
temp = node.cells[index].key
node.cells.pop(index)
node.num_of_cells -= 1
if node.num_of_cells == 0:
parent_index = bisect_left(node.parent.cells, temp, key=lambda x: x.key)
self._delete(node.parent, parent_index)
return True
The algorithm for this has again been adopted from Database Internals by Alex Petrov.
You can see a visual representation of the algorithm below.
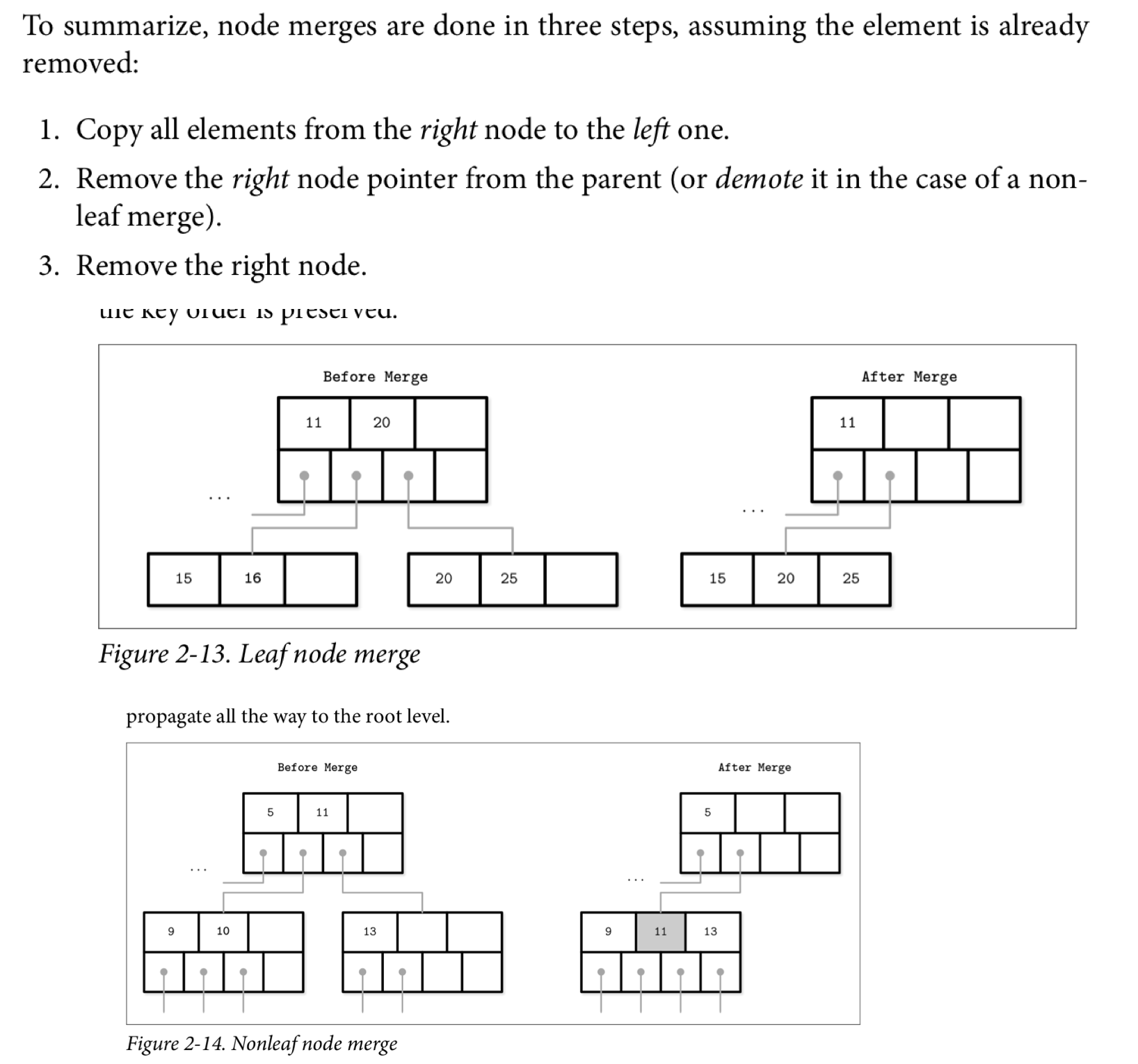
The algorithm basically copies all values from its right sibling pointer if it underflows and replaces it in an almost exact reversal of the split process when inserting a new value.
Conclusion
This concludes the second part of the B+ tree implementation. In the next part, I will be implementing everything we have discussed in C because that gives me more control over the file layout and the page cache.