Implementing B+ Trees In C

Introduction

In the last post, I went over a problem I faced with the invariants of the B+ tree. I also included an implementation of deleting keys & merging nodes from a B+ tree.

After getting the algorithm reasonably right in Python, I decided to implement it in C. One of the main reasons I wanted to do this is because it’s hard to see what the purpose of dividing a file into pages and implementing a page cache is when you’re working in Python.

Honestly, it was really hard because I don’t have too much experience in C but it was eye-opening. So, let’s dive in.

What Is A Page?

I kept reading about how B+ trees operate on nodes, which makes perfect sense. However, when you’re dealing with a lower level language like C, the terms nodes & pages become interchangeable. This kept confusing me until I went through with the implementation and it filled a lot of holes in my mental model.

Why Is A Page?

Before we jump into what a page is, let’s first explore why we need a page. Assume you have a computer with 1GB of RAM (bear with me here). Also assume that you have a binary file that is 24GB in size. Now, take a further leap and say that this computer runs without any OS overhead or additional processes eating into it’s RAM. The RAM is purely available for reading or writing to this file.

Now, let’s assume that we wanted to read a specific portion of this file. We could just find the offset of the portion we want to read from the beginning of the file and then do a disk seek. Great, we can read from the file.

Next, we want to write to a specific portion of the file. Again, we find the offset from the beginning of the file, do a disk seek and then write to the file. So, we have read & write operations. Essentially, what we have is a very slow database.

If you look at these latency numbers here, you’ll see that the latency of a disk seek is 100,000 times slower than the latency of a memory access.

So, if we wanted to make reading & writing faster, we’d try to do as much as we could in memory. However, we have a problem because our file size is 24GB and our RAM is 1GB. We can’t fit the entire file in memory. We can only fit 1/24th of the file in memory at a time.

This is where pages come in. We take the file and divide it into 24 equally sized chunks and call each one a page.

The image above shows what a file divided into pages looks like. You’ll notice that it is just a logical division of the file. In our example, the green lines correspond to the first GB of the page and the red lines correspond to the second GB of the page. There is no real demarcation between the first and the second page.

Now, we can fit one page in memory at a time. So, if we wanted to read the first page, we’d read the first GB of the file. If we wanted to read the second page, we’d read the second GB of the file but we’d have to evict the first GB of the file from memory.

The Relationship Between Pages & Nodes

Now that we know what a page is, let’s talk about what a node is. A node is a logical division of a page. So, each of our nodes is 1GB in size.

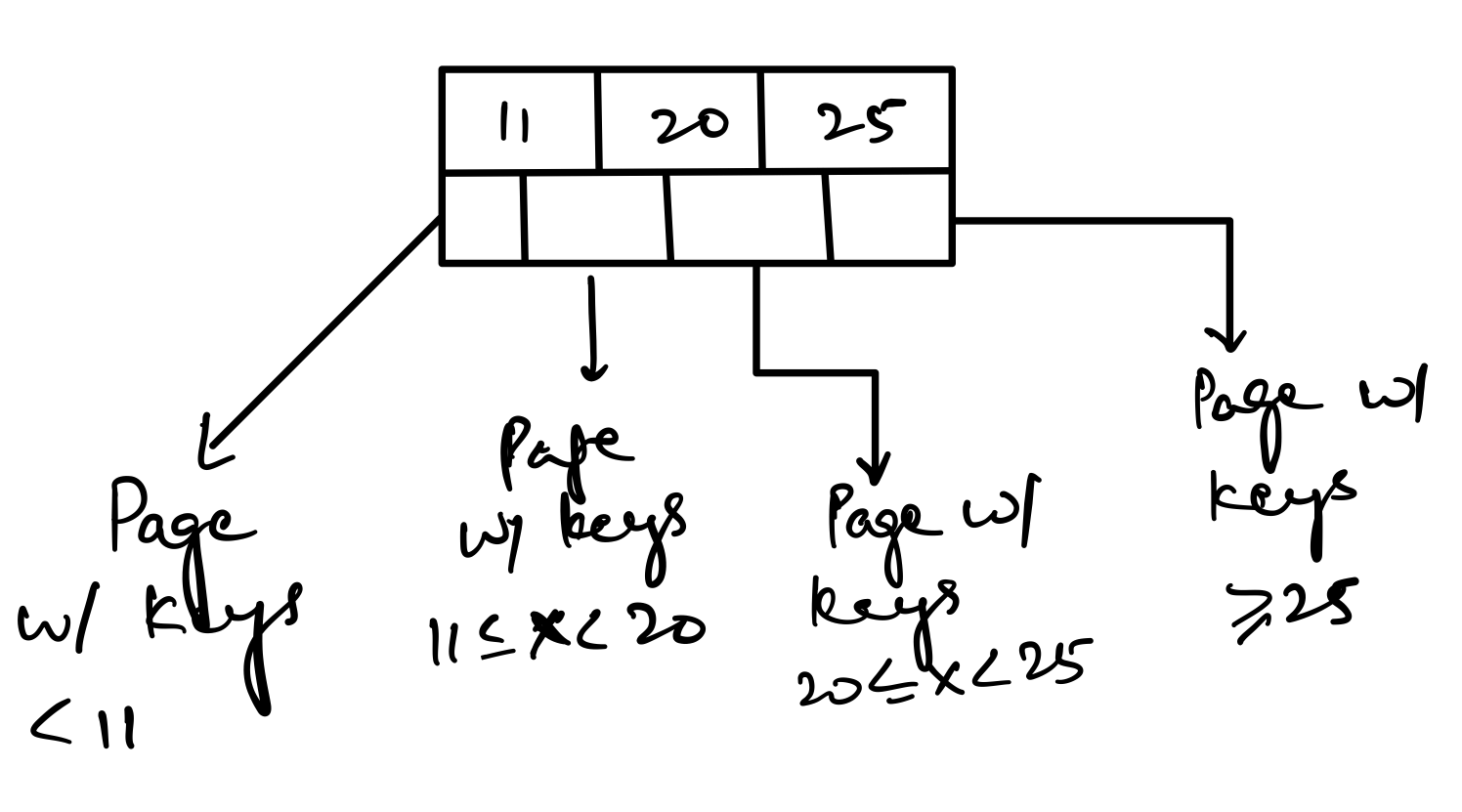
The image above shows a B+ tree node with 3 keys and 4 child pointers. Each node is equivalent to a page. So, in the root page, we have stored 3 keys and 4 child pointers. Each of the child pointers points to another page.

The Structure Of A Page

Let’s dive a little deeper into what a page looks like. Since this is an implementation detail, this is where database implementations will differ.

PostgreSQL

For instance, if you were to look at the structure of a PostgreSQL page here, you would notice some very explicitly defined sections like PageHeaderData, ItemIdData, Items etc.

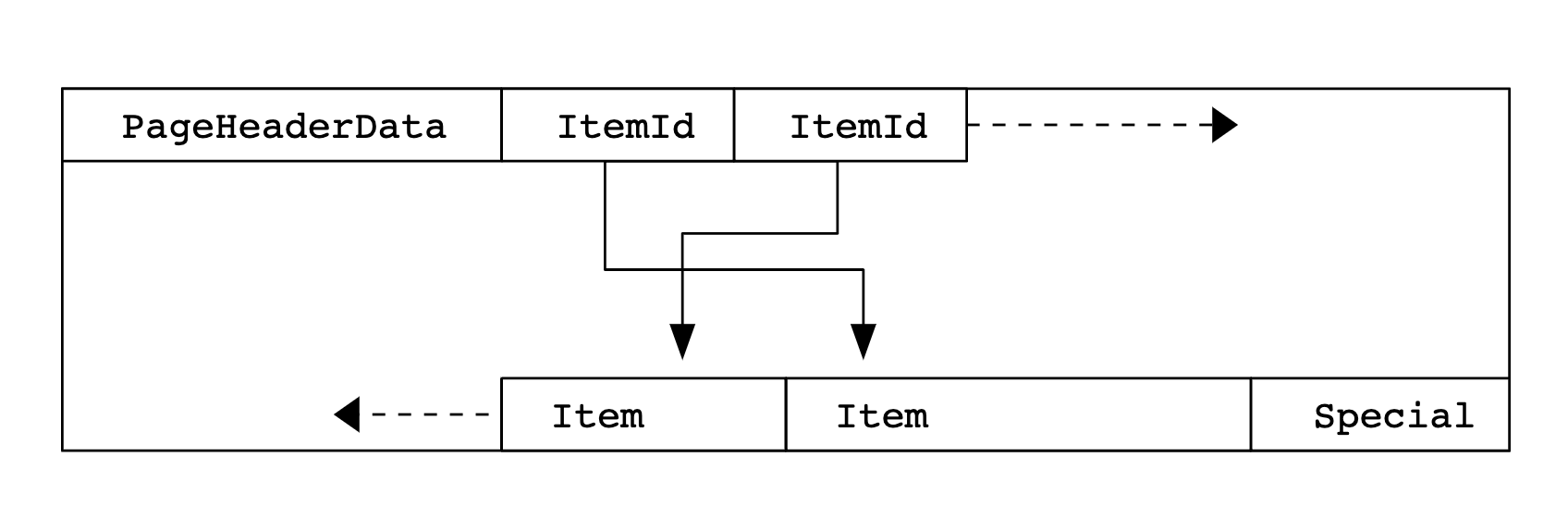
The image above shows how PostgreSQL defines ItemId pointers to the actual values stored in the page. For instance, if I were to store the values 1, 2, 3, 4, 5 in a page, I would have 5 ItemId pointers pointing to the values 1, 2, 3, 4, 5. This has the benefit of only modifying the pointers in the page when we want a sorted list of keys. There is less memory being moved around this way.

SQLite

If you were to look at the structure of a SQLite page here, you would notice that it is a lot more compact. It isn’t as comprehensive as a PostgreSQL page but it is a lot easier to implement.

My Implementation

I decided to go with a combination of both approaches. The format of my page header is defined below in C

/*
 * Common Node Header Layout
 */
const uint32_t NODE_TYPE_SIZE = sizeof(uint32_t);
const uint32_t NODE_TYPE_OFFSET = 0;
const uint32_t NODE_INITIALIZED_SIZE = sizeof(char);
const uint32_t NODE_INITIALIZED_OFFSET = NODE_TYPE_SIZE;
const uint32_t IS_ROOT_SIZE = sizeof(uint32_t);
const uint32_t IS_ROOT_OFFSET = NODE_TYPE_SIZE + NODE_INITIALIZED_SIZE;
const uintptr_t PARENT_POINTER_SIZE = sizeof(uintptr_t);
const uint32_t PARENT_POINTER_OFFSET = IS_ROOT_OFFSET + IS_ROOT_SIZE;
const uint16_t FREE_BLOCK_OFFSET_SIZE = sizeof(uint16_t);
const uint32_t FREE_BLOCK_OFFSET_OFFSET = PARENT_POINTER_OFFSET + PARENT_POINTER_SIZE;
const uint32_t COMMON_NODE_HEADER_SIZE =
    NODE_TYPE_SIZE + NODE_INITIALIZED_SIZE + IS_ROOT_SIZE + PARENT_POINTER_SIZE + FREE_BLOCK_OFFSET_SIZE;

I have a NODE_INITIALIZED flag that tells me if the node has been initialized. I set this to a specific char like ‘Y’ and look for that char when I want to check if the node has been initialized.

You might wonder why I didn’t just use a struct here. It’s mostly because I wanted to be explicit about the size of each field and I didn’t want to have to worry about padding and alignment issues. Now, since this isn’t a production implementation, obviously that doesn’t necessarily matter but while debugging I sometimes view the hex output of the database file and it’s easier to debug when I know exactly where each field is located.

Note: I’m sure debugging the hex output is a noob move. But, I’m a C noob. If anyone out there knows a better way, please let me know.

Here’s the rest of the page layout defined by sections

/**
 * @brief Internal Node Header Layout
 */
const uint32_t INTERNAL_NODE_NUM_KEYS_SIZE = sizeof(uint32_t);
const uint32_t INTERNAL_NODE_NUM_KEYS_OFFSET = COMMON_NODE_HEADER_SIZE;
const uintptr_t INTERNAL_NODE_RIGHT_CHILD_POINTER_SIZE = sizeof(uintptr_t);
const uint32_t INTERNAL_NODE_RIGHT_CHILD_POINTER_OFFSET = INTERNAL_NODE_NUM_KEYS_OFFSET + INTERNAL_NODE_NUM_KEYS_SIZE;
const uint32_t INTERNAL_NODE_HEADER_SIZE = COMMON_NODE_HEADER_SIZE + INTERNAL_NODE_NUM_KEYS_SIZE + INTERNAL_NODE_RIGHT_CHILD_POINTER_SIZE;

/**
 * Internal Node Body Layout
 */
const uintptr_t INTERNAL_NODE_CHILD_POINTER_SIZE = sizeof(uintptr_t);
const uint32_t INTERNAL_NODE_CHILD_POINTER_OFFSET = 0;
const uint32_t INTERNAL_NODE_KEY_SIZE = sizeof(uint32_t);
const uint32_t INTERNAL_NODE_KEY_OFFSET = INTERNAL_NODE_CHILD_POINTER_OFFSET + INTERNAL_NODE_CHILD_POINTER_SIZE;
const uint32_t INTERNAL_NODE_CELL_SIZE = INTERNAL_NODE_CHILD_POINTER_SIZE + INTERNAL_NODE_KEY_SIZE;

/**
 * Leaf Node Header Layout
 */
const uint32_t LEAF_NODE_NUM_CELLS_SIZE = sizeof(uint32_t);
const uint32_t LEAF_NODE_NUM_CELLS_OFFSET = COMMON_NODE_HEADER_SIZE;
const uint32_t LEAF_NODE_RIGHT_SIBLING_POINTER_SIZE = sizeof(uint32_t);
const uint32_t LEAF_NODE_RIGHT_SIBLING_POINTER_OFFSET = LEAF_NODE_NUM_CELLS_OFFSET + LEAF_NODE_NUM_CELLS_SIZE;
const uint32_t LEAF_NODE_HEADER_SIZE = COMMON_NODE_HEADER_SIZE + LEAF_NODE_NUM_CELLS_SIZE + LEAF_NODE_RIGHT_SIBLING_POINTER_SIZE;

/**
 * Leaf Node Body Layout
 */
const uint32_t LEAF_NODE_KEY_SIZE = sizeof(uint32_t);
const uint32_t LEAF_NODE_KEY_OFFSET = LEAF_NODE_HEADER_SIZE;
const uintptr_t LEAF_NODE_KEY_POINTER_SIZE = sizeof(uintptr_t);
const uint32_t LEAF_NODE_KEY_POINTER_OFFSET = LEAF_NODE_KEY_OFFSET + LEAF_NODE_KEY_SIZE;
const uint32_t LEAF_NODE_VALUE_SIZE = sizeof(Row);
const uint32_t LEAF_NODE_VALUE_OFFSET = PAGE_SIZE - LEAF_NODE_VALUE_SIZE;

You might notice that my keys aren’t just pointers. They have space to store a uint32_t data type and a pointer. The pointer points to the actual data. I only did this to make debugging simpler.

Page Size

How do you decide how many keys to store in a page? Well, for that, you first need to decide what the page size is. In my simple example above, I said the page size would be 1GB. That’s obviously incorrect. Deciding on the page size for a database engine depends on the OS the database intends to run on.

For instance, on my MacOS system, running PAGESIZE in the terminal shows me the size of the page is 16K bytes. In that case, my best bet would be to make the page size for my implementation 16K.

However, some Linux systems read & write to disk in 4K blocks as you can read here. Since most database engines are built to run on Linux, I imagine that’s why the default page size for most implementations is either 4K or 8K.

Page Cache

We’ve discussed what a page is and how it relates to the nodes of a B+ tree. We also discussed why we want to store data in pages because it allows us to manipulate them in memory. The question then becomes, how do we store pages in memory? We can use a data structure called a page cache.

The idea behind a cache is simple. When you request a specific page, the system will check to see if that page is already loaded into the cache. If it is loaded, it will return the page. If it isn’t loaded, it will load the page into the cache and then return the page. This is a lot faster than loading the page from disk every time you want to access it.

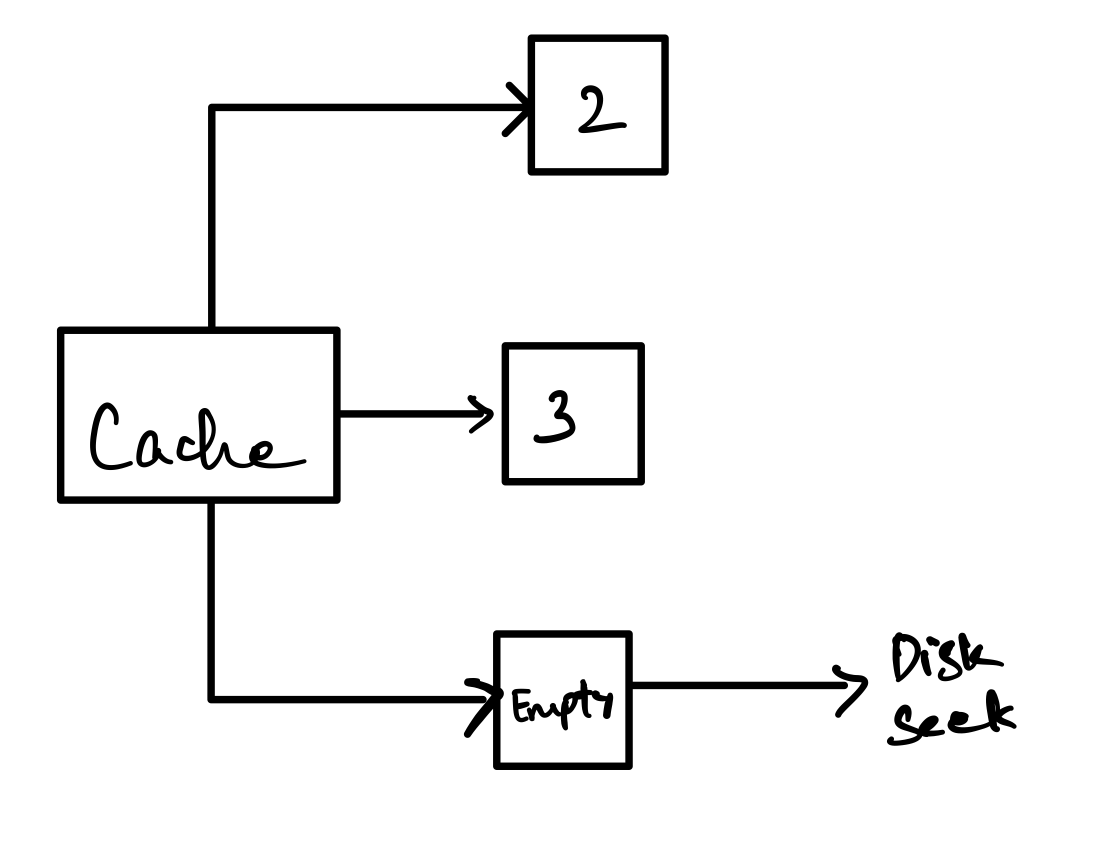
The image above shows a very simplified page cache. It has a fixed size and it stores pages in an array. When you request a page, it will check to see if the page is already loaded. If it is, it will return the page. If it isn’t, it will load the page into the cache and then return the page.

To simplify working with pages, I defined a struct called a Pager

typedef struct {
    int file_descriptor;
    uint32_t file_length;
    uint32_t num_pages;
    void* pages[MAX_NUM_OF_PAGES];
    uint32_t root_page_num;
} Pager;

Here’s the method to actually fetch the required page from the cache or failing that performing a disk seek to get the page into memory

void *get_page(Pager *pager, uint32_t page_num)
{
    if (pager->pages[page_num] == NULL)
    {
        void *page = malloc(PAGE_SIZE);
        uint32_t num_pages = pager->file_length / PAGE_SIZE;

        if (page_num <= num_pages)
        {
            lseek(pager->file_descriptor, page_num * PAGE_SIZE, SEEK_SET);
            ssize_t bytes_read = read(pager->file_descriptor, page, PAGE_SIZE);
            if (bytes_read == -1)
            {
                fprintf(stderr, "Error reading file: %d", page_num);
                exit(EXIT_FAILURE);
            }
        }
        pager->pages[page_num] = page;

        if (page_num >= pager->num_pages)
        {
            pager->num_pages = page_num + 1;
        }
    }
    return pager->pages[page_num];
}

Inserting A Node Into A B+ Tree

The method to insert a node into a B+ tree is defined here, which in turn calls a Generic.

void insert(Pager* pager, uint32_t key, uint32_t value) {
    //  get the root node
    void* node = get_page(pager, pager->root_page_num);
    printf("The root node is at %p\n", node);

    //  Check if the root node is initialized
    if (*(char*)node_initialized(node) != NODE_INITIALIZED) {
        initialize_leaf_node(node);
    }

    _insert(pager, node, key, value);
    return;

#define _insert(pager, node, key, value) \
    _Generic((value), \
        uint32_t: _insert_into_leaf, void*: _insert_into_internal)(pager, node, key, value)
}

This generic calls the correct method based on the type of the value. If the value is a uint32_t, it will call the _insert_into_leaf method. If the value is a void*, it will call the _insert_into_internal method.

void _insert_into_leaf(Pager* pager, void* node, uint32_t key, uint32_t value) {
    uint32_t num_cells = *(uint32_t*)leaf_node_num_cells(node);
    printf("The number of cells is %d\n", num_cells);

    //  Check if the node needs to be split
    if (num_cells < NODE_ORDER) {
        //  this leaf node does not need to be split
        printf("The leaf node does not need to be split\n");
        _insert_key_value_pair_to_leaf_node(node, key, value);
        return;
    }

    //  The node needs to split
    printf("The leaf node needs to be split\n");

    //  Check if this node has a parent that has been initialized
    void** parent_page_pointer = node_parent_pointer(node);

    if (*parent_page_pointer == NULL || *(char*)node_initialized(*parent_page_pointer) != NODE_INITIALIZED) {
        void* new_root = get_page(pager, pager->num_pages);
        *parent_page_pointer = new_root;
        initialize_internal_node(*parent_page_pointer);
        *(uint8_t*)node_is_root(*parent_page_pointer) = 1;
        set_root_page(pager, pager->num_pages - 1);
    }

    void* sibling_node = get_page(pager, pager->num_pages);
    split_leaf_node(pager, node, sibling_node, key, value);

    int key_to_promote = *leaf_node_key(sibling_node, 0);
    _insert(pager, *parent_page_pointer, key_to_promote, node);
    *node_parent_pointer(sibling_node) = *parent_page_pointer;
    *node_parent_pointer(node) = *parent_page_pointer;

    int parent_insertion_index = binary_search(*parent_page_pointer, key_to_promote);
    int parent_num_keys = *(uint32_t*)internal_node_num_keys(*parent_page_pointer);
    if (parent_insertion_index < parent_num_keys) {
        //  Set the left child pointer of the parent at  insertion index equal to the sibling node
        *internal_node_child_pointer(*parent_page_pointer, parent_insertion_index) = sibling_node;
    } else {
        //  Set the right child pointer of the parent at insertion index equal to the sibling node
        *internal_node_right_child_pointer(*parent_page_pointer) = sibling_node;
    }

    return;
}

Here is the imeplementation of the _insert_into_internal method

void _insert_into_internal(Pager* pager, void* node, uint32_t key, void* child_pointer) {
    uint32_t num_keys = *(uint32_t*)internal_node_num_keys(node);
    printf("The number of keys is %d\n", num_keys);

    //  Check if the node needs to be split
    if (num_keys < NODE_ORDER - 1) {
        printf("The internal node does not need to be split\n");
        _insert_key_value_pair_to_internal_node(node, key, child_pointer);
        return;
    }

    //  The node needs to be split

    //  Check if this node has a parent that has been initialized
    void** parent_page = node_parent_pointer(node);

    //  Create a new root if the parent has not been initialized
    if (*(char*)node_initialized(*parent_page) != NODE_INITIALIZED) {
        void* new_root = get_page(pager, pager->num_pages);
        *parent_page = new_root;
        initialize_internal_node(*parent_page);
        *(uint8_t*)node_is_root(parent_page) = 1;
        set_root_page(pager, pager->num_pages - 1);
    }

    printf("The internal node needs to be split\n");
    void* sibling_node = get_page(pager, pager->num_pages);
    split_internal_node(pager, node, sibling_node, key, child_pointer);
    if (key <= *internal_node_key(sibling_node, 0)) {
        _insert(pager, node, key, child_pointer);
    } else {
        _insert(pager, sibling_node, key, child_pointer);
    }

    int key_to_promote = *internal_node_key(sibling_node, 0);
    _insert(pager, parent_page, key_to_promote, sibling_node);
    *node_parent_pointer(sibling_node) = parent_page;
    *node_parent_pointer(node) = parent_page;

    int parent_insertion_index = binary_search(parent_page, key_to_promote);
    int parent_num_keys = *(uint32_t*)internal_node_num_keys(parent_page);
    if (parent_insertion_index < parent_num_keys) {
        void** parent_child_pointer = internal_node_child_pointer(parent_page, parent_insertion_index);
        *parent_child_pointer = sibling_node;
    } else {
        void** parent_right_child_pointer = internal_node_right_child_pointer(parent_page);
        *parent_right_child_pointer = sibling_node;
    }

    //  For an internal node, remove the node's right child pointer
    void** right_child_pointer = internal_node_right_child_pointer(node);
    *right_child_pointer = NULL;
    return;
}

The basic idea behind the algorithm is the same as the one implemented in Python in earlier posts. However, there are some intricacies in how paging is handled when a language like C.

You will notice accessor methods all over the place like internal_node_key for example. This is a simple method that will calculate the offset to a specific region in memory and return a pointer to that region. Here’s the implementation for that method

uint32_t* internal_node_key(void* node, uint32_t key_num) {
    return node + INTERNAL_NODE_HEADER_SIZE + (key_num * INTERNAL_NODE_CELL_SIZE) + INTERNAL_NODE_CHILD_POINTER_SIZE;
}

I am not going into the details of splitting & merging nodes here. I will cover that in a future post. However, if you want to view the entire code base, you can find it here.

Note: I took pieces of code from different blog posts and used that to build my own implementation. I would highly recommend going through this blog post. It is a great resource for learning how to build a database from scratch.